Landslide hazard assessment using Monte Carlo simulation

ABSTRACT: Evaluating the stability of variable landforms is important for land management planning on forest lands in the western United States and Alaska. This paper describes a rational means for considering both natural variability and measurement uncertainty in landslide hazard evaluation of both natural slopes, and constructed cut and fill slopes. Monte Carlo simulation is used to simulate the frequency distribution of the factor of safety on a given landform or slope. The probability of failure is taken as the relative frequency with which the factors of safety are less than or equal to one. The simulation program is written for IBM-PC's and compatibles, includes a menu-driven user interface, and allows the use of seven different input probability distributions to describe the natural variability and uncertainty of each input variable.

1. INTRODUCTION

Many forest lands in the western United States and Alaska are classified as potentially unstable. Unless carefully planned and executed, timber harvesting operations, road construction or other land management activities in these areas can accelerate mass failure and may cause significant impacts on soil productivity and water quality. Accurate assessment of potential landslide hazard early in the planning process is essential. We believe a geotechnical stability model approach for hazard assessment has advantages over subjective or statistical approaches (e.g. Roth 1983) because it is widely applicable (model-based, not data-based), and because it can be used for sensitivity studies and to predict the effects of managerial actions. We also believe that a probabilistic approach is essential when rationally considering the natural variability and uncertainty of each input variable in a stability analysis. This paper describes two microcomputer programs, LISA and SARA, which use Monte Carlo simulation to help quantify the probability of slope failure for both natural and man-made slopes and to assess the effect of management activities such as timber harvest.

2. MONTE CARLO SIMULATION

Monte Carlo simulation is useful for modeling an attribute that cannot be sampled or measured directly, but can be expressed as a mathematical function of properties that can be sampled. Factor of safety fits this situation. Although other probabilistic methods are available for estimating landslide failure probabilities (e.g. Chowdhury and Tang 1987), Monte Carlo simulation is the method used in LISA and SARA because it allows all input variables to be treated stochastically, as is necessary for a realistic stability assessment of large landforms where all variables can have significant spatial variability and measurement uncertainty.
    If we want to predict a possible value of the factor of safety, we take a possible value for each input variable and use an appropriate equation to calculate the corresponding factor of safety value. This is known as one Monte Carlo pass or iteration. In Monte Carlo simulation we generate a considerable number of factor of safety values, say 1000, by repeated random, independent samplings of a set of possible input values, and then calculate the corresponding factor of safety value for each pass. The set of possible input values is described by a probability distribution for each input variable. In the LISA and SARA computer models, the user may choose a constant value or a uniform, normal, lognormal, triangular, beta, histogram, or bivariate normal probability distribution. The result is 1000 possible factor of safety values that can be displayed as a histogram; the probability of failure (P_ƒ ) then is obtained by dividing the total number of passes into the number of calculated factor of safety values which are less than or equal to one.

2.1 The performance functions

The LISA and SARA computer models use the infinite slope model as the performance function to analyze the stability of natural slopes, and stability number charts developed by Cousins (1978) and quantified by Pyles and others (1984) to analyze the stability of man-made slopes, such as road cut and fill slopes or embankments. The infinite slope equation used in the computer models is:

where FS is the factor of safety, α is the slope of the ground surface in degrees, D is the total soil thickness, D_w is the saturated soil thickness, C_r is the tree root strength expressed as a cohesion, q_o is tree surcharge, C_s is soil cohesion which can include both true soil cohesion and apparent soil cohesion due to capillary suction (C_app), φ′ is effective angle of internal friction, γ is moist soil unit weight, γ_sat is saturated soil unit weight, and γ_w is the unit weight of water (9.81 kN/m³). The Cousins equation is:

where k is an empirical coefficient developed by Prellwitz (1988), as discussed below; N_ƒ  is Cousins' stability number; C is cohesion which can include both C_s and C_r; γ is moist soil unit weight; and h is vertical height of the cut or fill. The user may either specify h, or specify the cut and fill slope ratios and road and ditch widths and the program will determine h by superimposing a full bench, through fill, or self-balanced road prism on the natural slope.
   Both models are well suited to Monte Carlo simulation because the critical failure surfaces are assumed—the infinite slope model assumes a planar failure surface (typically the bedrock surface) which is parallel to both the ground surface and the phreatic surface, and the Cousins' method assumes a circular arc exiting at the slope toe. Although both models tend to oversimplify in situ conditions, they have been found to be adequate for planning purposes (Prellwitz and others 1983, Sidle and others 1985); however, Cousins' stability number charts do require modification to account for sloping bedrock and phreatic surfaces typically found in mountainous terrain. This modification is accounted for by the empirical factor, k, which relates the factor of safety estimated using Cousins' charts to the critical failure circle (with a factor of safety of 1.00) found using modified Bishop analysis for a variety of typical slope, groundwater height and soil shear strength conditions (Prellwitz 1988).

2.2 Correlation between variables

To achieve a realistic simulation using Monte Carlo methods, the relationships between dependent variables must be taken into account. The variables treated as dependent in the LISA and SARA models are C_s and φ′, and dry unit weight (γ_d) and φ′.
    Although there exists some contradiction in the literature, C_s and φ′ generally are considered to be inversely related with reported correlation coefficients (r ) of -0.2 to -0.85 (Cherubini and others 1983). If this correlation is not considered in the simulation, soil shear strength can be significantly overestimated and underestimated, resulting in an increase in variance of simulated shear strength. The bivariate normal probability density function (PDF) can be used in LISA and SARA to model C_s—φ′ dependence.
    The second relationship considered by LISA and SARA is the positive correlation that exists between γ_d and φ′. The models handle this correlation very simplistically by using the same random number to sample from the univariate distributions for γ_d and φ′; therefore, when a high value is sampled for γ_d, a high value is sampled for φ′ to model the desired proportional relationship. This method produces r values between γ_d and φ′ of 0.95 to 1.0 (with 1.0 occurring when the same distribution type is used for both variables). This degree of correlation is greater than typically found in nature; however, because the infinite slope equation is generally insensitive to γ_d, the P_ƒ  values are affected only slightly.
    Dependence between other variables, such as an inverse relationship between soil depth and ground slope, is sometimes observed. At this time, LISA and SARA do not have the capability of allowing the user to enter a functional relationship between selected variables to model such correlations in a rigorous manner. Instead, the user must subdivide geomorphic landforms into smaller units with narrow ranges of input values, so that within those ranges, one could expect all other variables to be independent.

3. MEANING AND USE OF THE PROBABILITY OF FAILURE

The P_ƒ , strictly speaking, is the total number of Monte Carlo iterations divided into the number of calculated factors of safety with a value less than or equal to one; however, it is common to view the probability of an event as the likelihood of that event occurring. This meaning does not work well for the P_ƒ  of a large, variable landform, because the event of one failure occurring in a landform or along a proposed road location gives a probability of landslide occurrence of one. It is more useful to think of the P_ƒ  as the relative frequency of failure events in the analysis area or along the road location. The P_ƒ  then can be used qualitatively to make relative comparisons between landforms or road locations to identify areas that should be targeted for additional analysis. The P_ƒ  can be viewed as the probability of landslide occurrence if the area analyzed is small enough (i.e., one slope or one drainage) so that only one failure could physically occur within that area.
   Typically in hazard assessments for planning purposes, information comes primarily from soils and geology inventories and aerial photo interpretation, with few actual field measurements. In this case, the input distributions represent one's uncertainty about the variables as well as one's best guess about their spatial variability across the landform; therefore, because of the two-dimensional nature of the infinite slope analysis, the estimated P_ƒ  can best be thought of as the likelihood that any possible randomly selected cross-section through the slope would be analyzed as unstable. As more data are available, the probability distributions of each input variable represents more the spatial variability of that variable and less the uncertainty. Here the P_ƒ  should be an estimate of the expected percentage of area of the landform or of the length of the roadway involved in failure during the period appropriate to the analysis — for example, during the period of minimum root strength following timber harvest, or during the rain or snow melt event causing the groundwater levels used in the analysis. This interpretation of the P_ƒ  can help geotechnical specialists recommend to land managers what level of P_ƒ  is excessive because percentage area or road length in failure can be used to evaluate the possible consequences of failure, such as an estimate of the quantity of material that may impact downslope lands or streams.
    The P_ƒ  estimated using LISA and SARA should be reported as a conditional probability given that the groundwater distribution used in the analysis (which is in part dependent on climatic events and thus has its own probability of occurrence) does indeed occur. The P_ƒ  also should be verified as reasonable by comparison with field observations of slope instability. Used as an iterative tool, LISA and SARA can help the user document personal judgments and observations about an area or road location, communicate them to land managers and to other geotechnical specialists, and help identify factors critical to landslide hazard assessment in a given area. The P_ƒ  also can be used quantitatively in a risk analysis, such as an expected monetary value (EMV) decision analysis. Research efforts are continuing in this area.
    LISA and SARA do not simulate the sizes, numbers, locations or types of failure that might occur (although LISA gives more accurate results for translational failure modes, and SARA can give an indication as to whether the failure mode is more likely to be translational or circular). Therefore, LISA and SARA cannot be used to estimate directly the consequences of failure, such as whether sediment will reach a stream, or the volume of sediment delivered.

4. EXAMPLE APPLICATION

The Clearwater National Forest in northern Idaho planned to construct a road from an existing ridge-top road to the North Fork of the Clearwater River, which flows into Dworshak Reservoir. The proposed road location crossed three landforms— mountain slopelands (31), mass-wasted slopes (50), and nondissected stream breaklands (60), as shown in figure 1 (Wilson and others 1983). The mountain slopelands consist of the lower and middle slopes of mountains and primary ridges along the North Fork of the Clearwater River. Soil thickness of 1.5 to 2.5m and slope gradients of 30 to 60% were anticipated. Groundwater levels were expected to be high due to concentrated flow by landform shape and low slope position. The areas mapped as mass-wasted slopes were classified based on benched, hummocky topography observed in aerial photographs rather than observations of recent failures. Highly variable soil thicknesses, slope gradients and groundwater concentrations were anticipated. As might be expected, the Forest land managers were concerned about crossing this landform. In the nondissected stream breaklands, soils were expected to be thin (less than 1.5m), groundwater levels low, and slopes steep (greater than 60%). The bedrock underlying the entire area is micaceous schist which commonly produces cohesionless (nonplastic) silty sands and gravel soils. Large differences in shear strength across the area were not anticipated.

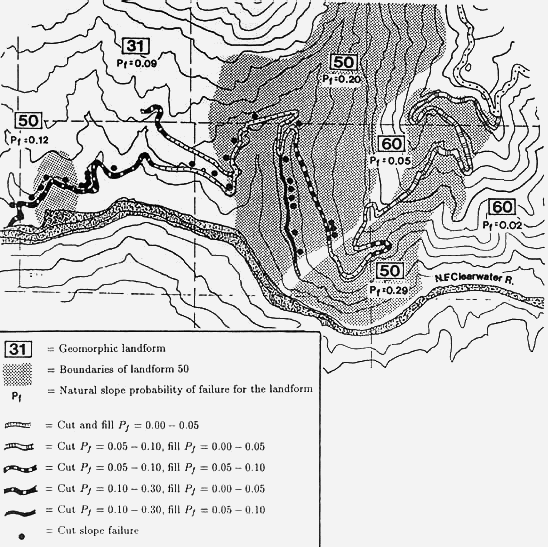
Figure 1 — Example problem showing natural slope P_ƒ  values estimated using LISA, and cut-and-fill slope P_ƒ  values estimated using SARA. Also shown are locations of cutslope failures which occurred the first spring after construction. No fill slope failures occurred.

Based on this inventory information, values and probability distributions were selected for each input variable in the infinite slope equation and the P_ƒ  estimated using LISA; the P_ƒ  values are shown on figure 1 with the landform types. As one might expect, landform 50 (interpreted as mass-wasted slopes) had the highest probabilities of failure with values ranging from 0.12 to 0.29.
   The relatively high P_ƒ  values and the topographic indications of past failure activity in landform 50 prompted the Forest land managers to request further analysis of the proposed road location. A field reconnaissance of the road location provided measurements of slope gradient, and estimates of soil thickness and groundwater conditions. The road was divided into 12 segments based on similar landform, slope and drainage characteristics. Within each segment, typical cross sections of the natural slope were measured and a self-balanced road prism superimposed. Cut slopes of 3/4:1 to 1:1 and fill slopes of 1.5:1 were used for this analysis. The probabilities of failure for both the natural slope immediately above the road and for the road prism were estimated for each road segment using the SARA program. Generally, the road was well located—on less steep slopes and avoiding obvious wet areas—which resulted in lower natural slope P_ƒ  values along the road location than for the landform as a whole. The road location and the resulting P_ƒ  values for the cut-and-fill slopes of the road are also shown on figure 1.
    Although there was relatively high failure potential in some road segments, other important factors lead the Forest to decide to proceed with road project; however, the hazard analysis provided valuable input to the Forest land managers, particularly in increased awareness of the landslide potential, so that possible consequences and mitigation measures could be considered. As a result of this analysis, design alterations were made to reduce the hazard in some segments.
    In the spring following road construction, 28 cutslope failures and no fillslope failures were observed. One third of the cutslope failures fell into each of three size classes—10 to 50m³, 50 to 100m³, and 100 to 300m³. The failure locations are shown by the dots in figure 1. Qualitatively, SARA estimated the likelihood of failure for the cutslope well—18 of the failures occurred in landform 50 which the model showed to have the highest P_ƒ ; however, there were segments in landform 50 that showed moderate hazard and no failures occurred, and segments in landforms 31 and 50 that showed low hazard and 7 failures occurred. We believe the discrepancies are due to inaccuracies in describing the actual in situ conditions. The results of this example illustrate that even probabilistic models provide "good" hazard assessments only to the extent that the input distributions adequately describe actual field conditions. Post-construction inspection to compare input distributions used with conditions observable in road cuts provide invaluable information that then can be used to improve future assessments in similar areas. Feedback of this type is essential for obtaining realistic results. Research is continuing in the areas of updating input distributions using Bayesian techniques, but currently distributions are updated subjectively.
    Although not addressed in this example, LISA can be used to evaluate the effects of timber harvest by reducing the values of tree root strength and increasing the values for groundwater used in the analysis to model the effects of timber removal (Hammond and others 1991).

5. CONCLUSIONS

The LISA and SARA programs are tools to assist the user in understanding the factors affecting slope stability, quantifying observations and judgments regarding stability, and in documenting and communicating those observations and judgments to other geotechnical specialists and to land managers. As with any computer program, varying answers can be obtained by altering the input data, so caution must be exercised to prevent the analysis from becoming a game of numbers. The input data should be based on sound geotechnical observations, interpretations, and measurements by qualified individuals who have a thorough understanding of the model; and the results compared to actual field conditions to assure that they are indeed reasonable.

The primary advantages of the probabilistic models described in this paper are

1. they provide a rational, objective framework for the probabilistic stability assessment of slopes and road ways,
2. they allow the user to treat all input variables stochastically,
3. they provide a documented plan for how uncertainty and variability are considered, and
4. they provide output critical for economic studies and risk analyses.

Because the models are based on geotechnical stability models, they can be used as a design aid, and allow data obtained in geotechnical design and construction projects to be used in future hazard analysis for planning purposes. In addition, the computer programs are designed so that they are easy to understand and use with minimal training in probabilistic concepts.
    The programs assist the user in estimating only the landslide hazard; however, the consequences of slope failure (such as the potential for damage to timber and fisheries resources, roads or structures, or the potential for injury or loss of life) should be assessed by the user to provide a complete risk analysis.

ACKNOWLEDGMENTS

David Hall, Paul Swetik and Scott Kendall designed the user interfaces and coded the LISA and SARA computer programs. Richard van Dyke assisted in SARA algorithm development. Gordon Booth initially suggested the Monte Carlo approach. Many geotechnical and engineering geology specialists throughout the Forest Service assisted in the field testing of LISA and SARA and have provided valuable feedback throughout program development.

REFERENCES

Chowdhury, R.N. & W.H. Tang 1987. Comparison of risk models for slopes. Proc. 5th ICASP: 863-869. Vancouver, B.C.: Institute for Risk Research, University of Waterloo.

Cousins, B.F. 1978. Stability charts for simple earth slopes. ASCE, J. Geotechnical Eng. Div. 104(GT2): 267-279.

Hammond, C.J., D.E. Hall, S.M. Miller, & P.G. Swetik 1991. Level I stability analysis (LISA) documentation for version 2.0. USDA Forest Service, General Tech. Report INT-in press.

Prellwitz, R.W. 1988. "SSIS" and "SSCHFS"— preliminary slope stability analyses with the HP41 programmable calculator. U.S. Department of Agriculture, Forest Service, Engineering Staff, Washington, D.C.: EM-7170-9.

Prellwitz, R.W., T.R. Howard & W.D. Wilson 1985. Landslide analysis concepts for management of forest lands on residual and colluvial soils. Transportation Research Record 919: 27-36.

Pyles, M.R., W.L. Schroeder & R.C. Pratt 1984. Simplified stability assessment for low-volume road cut and fill slopes. Oregon State Univ. final report on USDA, Forest Service Res. Ag. Suppl. No. PNW-82-326.

Roth, R.A. 1983. Factors affecting landslide-susceptibility in San Mateo County, CA. Bull. of the Assoc. of Eng. Geologists 10(4): 353-372.

Sidle, R.C., A.J. Pearce & C.L. O'Loughlin 1985. Hillslope stability and land use. Water Resources Monograph series No. 11: American Geophysical Union: Washington, DC.

Wilson, D., J. Coyner & T. Dechert 1983. Land system inventory of the Clearwater National Forest, Region 1—first review draft. U.S. Department of Agriculture, Forest Service.

Hammond, C.J.; Prellwitz, R.W.; Miller, S.M. 1991. Landslide hazard assessment using Monte Carlo simulation. Bell, D.H., ed. Landslides/Glissements de terrain. Proceedings of the Sixth International Symposium, 10-14 February 1992, Christchurch, New Zealand. Rotterdam, The Netherlands: A.A. Balkema. Vol. 2, 959-964.

USDA Forest Service Rocky Mountain Research Station Moscow Forestry Sciences Laboratory 1221 South Main Street, Moscow, ID 83843 https://forest.moscowfsl.wsu.edu/